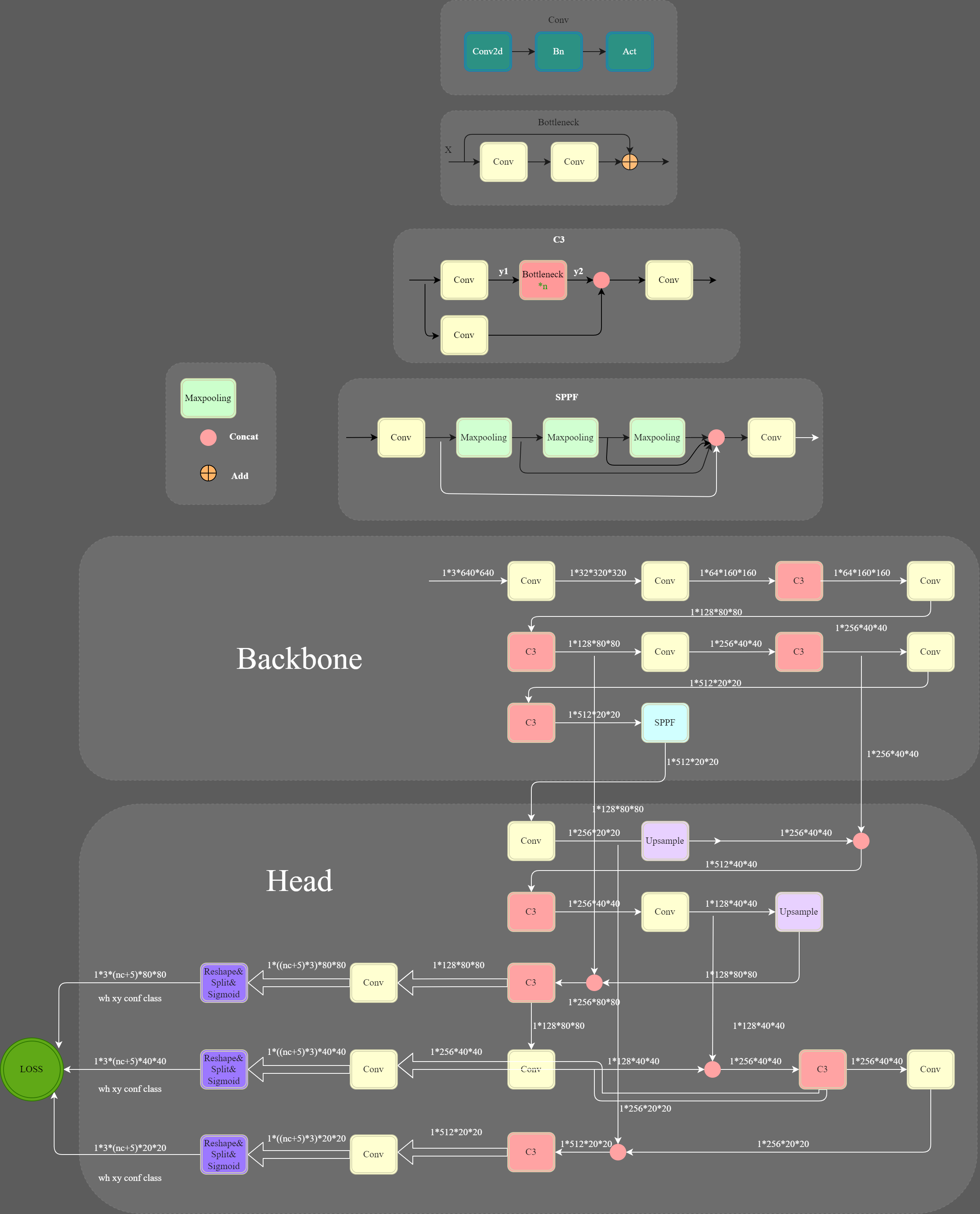
高斯滤波和均值滤波
高斯滤波
二维高斯分布密度函数 \[ G(x,y) = \frac{1}{2\pi\sigma^{2}}{}e^{-\frac{x^{2}+y^{2}}{2\sigma^{2}}} \] 高斯滤波的核心是以高斯分布样式生成权重的图像卷积,区域不够则用0去填补。
例如一个3*3的高斯核,一旦指定了$ $
的大小,9个点的权重也将唯一确定。
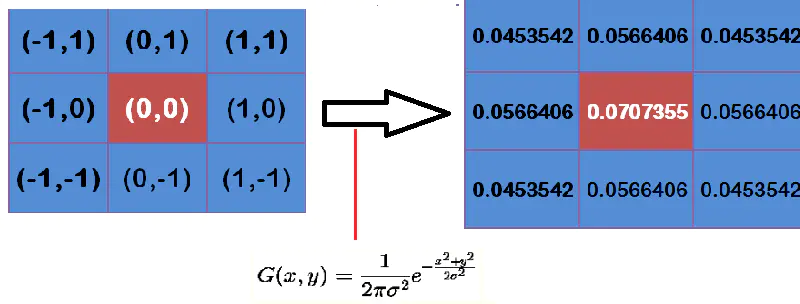
然后对图像进行卷积,生成新的图像。
高斯滤波的核心在于假如出现了噪声点,周围都是正常点,那么噪声点会被加权之后稀释,也就起到了滤波的作用。
性质:
高斯滤波的分离性质 (得规定 \(\sigma\) 相同)。 \[ G(x,y) =\frac{1}{2\pi\sigma^{2}}{}e^{-\frac{x^{2}+y^{2}}{2\sigma^{2}}}\\ =\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{x^{2}}{2\sigma}}\cdot{\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{y^{2}}{2\sigma}}} \\ = G(x)\cdot{G(y)} \] 这里$ G(x) $ 和 $ G(y)$ 分别是 $ x$, $ y$ 轴上的高斯分布密度函数
假定二维高斯的核大小为
(2m+1)*(2n+1),这里为了方便起见规定核的尺寸为奇数, 对于原图的任意一点 \((x_m,y_n)\),以\((x_m,y_n)\) 为中心大小(2m+1)*(2n+1)的区域不妨记为: \[ A=\left[ \begin{array}{} (x_{0},y_{0}) & ... & (x_{0},y_{n-1}) & (x_{0},y_{n}) & (x_{0},y_{n+1}) & ... & (x_{0},y_{2n})\\ ... & ... & ... & ... & ... & ... & ...\\ (x_{m-1},y_{0}) & ... & (x_{m-1},y_{n-1}) & (x_{m-1},y_{n}) & (x_{m-1},y_{n+1}) & ... & (x_{m-1},y_{2n})\\ (x_{m},y_{0}) & ... & (x_{m},y_{n-1}) & (x_m,y_n) & (x_{m},y_{n+1}) & ... & (x_{m},y_{2n})\\ (x_{m+1},y_{0}) & ... & (x_{m+1},y_{n-1}) & (x_{m+1},y_{n}) & (x_{m+1},y_{n+1}) & ... & (x_{m+1},y_{2n})\\ ... & ... & ... & ... & ... & ... & ...\\ (x_{2m},y_{0}) & ... & (x_{2m},y_{n-1}) & (x_{2m},y_{n}) & (x_{2m},y_{n+1}) & ... & (x_{2m},y_{2n})\\ \end{array} \right ] \] 也约定高斯核为 \(G(x,y)_{2m+1,2n+1}\) \[ G_{2m+1,2n+1} = [{g_{i,j}}]_{2m+1,2n+1} \] 其中: \[ g_{i,j} = G(i-m,j-n) \]该区域的图像像素值为: \[ S = [s_{i,j}]_{2m+1,2n+1} \] 特殊的点 $ (x_m,y_n)$ 的像素为 $ s_{m,n}$
只经过二维高斯过滤后点 $(x_{m},y_{n}) $ 像素变为 \[ s_{m,n}^{'}=\frac{1}{(2m+1)(2n+1))}\sum_{p=0}^{2m+1}\sum_{q=0}^{2n+1}{s_{p,q}\cdot{g_{p,q}}} \]
如果原图经过 \(x\) 轴的高斯滤波核大小为 \(2m+1\) ,其中: \[ G_{x}(x)=\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{x^{2}}{2\sigma}} \] 于是点图像变为一个长为 $ 2n +1$ 的向量。不妨记为 $ = [y_0,...,y_{2n+1}]^{T}$
其中 \[ y_{i} = \frac{1}{2m+1}\sum_{k=0}^{2m+1}{G_{x}(i-m)\cdot{s_{k,i}}} \] 再经过\(y\) 轴的高斯滤波核大小为 \(2n+1\) 其中: \[ G_{y}(y)=\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{y^{2}}{2\sigma}} \]
\[ s_{m,n}^{''}=\frac{1}{2n+1}\sum_{q=0}^{2n+1}{y_q\cdot{G_y(q-n)}}\\ =\frac{1}{(2m+1)(2n+1))}\sum_{q=0}^{2n+1}{\sum_{k=0}^{2m+1}{G_x{(i-m)}G_y{(q-n)}}\cdot{s_{k,q}}}\\ =\frac{1}{(2m+1)(2n+1))}\sum_{k=0}^{2m+1}{\sum_{q=0}^{2n+1}{G_x{(i-m)}G_y{(q-n)}}\cdot{s_{k,q}}}\\ =\frac{1}{(2m+1)(2n+1))}\sum_{k=0}^{2m+1}{\sum_{q=0}^{2n+1}}{G(i-m,q-n)\cdot{s_{k,q}}}\\ =\frac{1}{(2m+1)(2n+1))}\sum_{k=0}^{2m+1}{\sum_{q=0}^{2n+1}}{s_{k,q}\cdot{g_{k,q}}}=s_{m,n}^{'} \]
$ Q E D$
均值滤波
均值滤波则可认为高斯核里值恒为1的滤波方式。
test image

测试
$ 18+15 $
$ x^2 $
$ f $
1 | $$\begin{equation} |
\[sin^2\theta + cos^2\theta = 1\]
$ H( X ) =-_{i=1}^n{p( x_i ) p( x_i )}$
\[ H\left( X \right) =-\sum_{i=1}^n{p\left( x_i \right) \log p\left( x_i \right)} \] \[ H\left( X \right) =-\sum_{i=1}^n{p\left( x_i \right) \log p\left( x_i \right)} \]
Hello World
Welcome to Hexo! This is your very first post. Check documentation for more info. If you get any problems when using Hexo, you can find the answer in troubleshooting or you can ask me on GitHub.
Quick Start
Create a new post
1 | $ hexo new "My New Post" |
More info: Writing
Run server
1 | $ hexo server |
More info: Server
Generate static files
1 | $ hexo generate |
More info: Generating
Deploy to remote sites
1 | $ hexo deploy |
More info: Deployment
决策树
# 决策树