高斯滤波
二维高斯分布密度函数 \[ G(x,y) = \frac{1}{2\pi\sigma^{2}}{}e^{-\frac{x^{2}+y^{2}}{2\sigma^{2}}} \] 高斯滤波的核心是以高斯分布样式生成权重的图像卷积,区域不够则用0去填补。
例如一个3*3的高斯核,一旦指定了$ $
的大小,9个点的权重也将唯一确定。
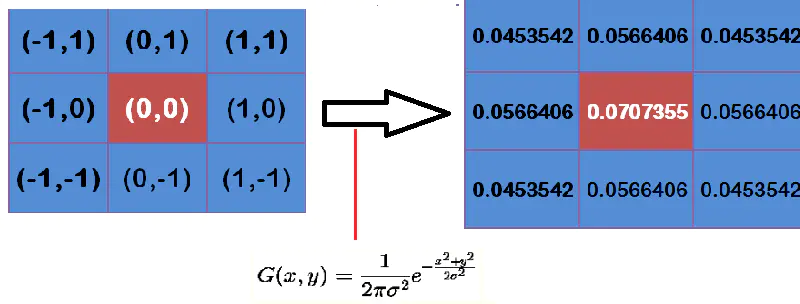
然后对图像进行卷积,生成新的图像。
高斯滤波的核心在于假如出现了噪声点,周围都是正常点,那么噪声点会被加权之后稀释,也就起到了滤波的作用。
性质:
高斯滤波的分离性质 (得规定 \(\sigma\) 相同)。 \[ G(x,y) =\frac{1}{2\pi\sigma^{2}}{}e^{-\frac{x^{2}+y^{2}}{2\sigma^{2}}}\\ =\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{x^{2}}{2\sigma}}\cdot{\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{y^{2}}{2\sigma}}} \\ = G(x)\cdot{G(y)} \] 这里$ G(x) $ 和 $ G(y)$ 分别是 $ x$, $ y$ 轴上的高斯分布密度函数
假定二维高斯的核大小为
(2m+1)*(2n+1),这里为了方便起见规定核的尺寸为奇数, 对于原图的任意一点 \((x_m,y_n)\),以\((x_m,y_n)\) 为中心大小(2m+1)*(2n+1)的区域不妨记为: \[ A=\left[ \begin{array}{} (x_{0},y_{0}) & ... & (x_{0},y_{n-1}) & (x_{0},y_{n}) & (x_{0},y_{n+1}) & ... & (x_{0},y_{2n})\\ ... & ... & ... & ... & ... & ... & ...\\ (x_{m-1},y_{0}) & ... & (x_{m-1},y_{n-1}) & (x_{m-1},y_{n}) & (x_{m-1},y_{n+1}) & ... & (x_{m-1},y_{2n})\\ (x_{m},y_{0}) & ... & (x_{m},y_{n-1}) & (x_m,y_n) & (x_{m},y_{n+1}) & ... & (x_{m},y_{2n})\\ (x_{m+1},y_{0}) & ... & (x_{m+1},y_{n-1}) & (x_{m+1},y_{n}) & (x_{m+1},y_{n+1}) & ... & (x_{m+1},y_{2n})\\ ... & ... & ... & ... & ... & ... & ...\\ (x_{2m},y_{0}) & ... & (x_{2m},y_{n-1}) & (x_{2m},y_{n}) & (x_{2m},y_{n+1}) & ... & (x_{2m},y_{2n})\\ \end{array} \right ] \] 也约定高斯核为 \(G(x,y)_{2m+1,2n+1}\) \[ G_{2m+1,2n+1} = [{g_{i,j}}]_{2m+1,2n+1} \] 其中: \[ g_{i,j} = G(i-m,j-n) \]该区域的图像像素值为: \[ S = [s_{i,j}]_{2m+1,2n+1} \] 特殊的点 $ (x_m,y_n)$ 的像素为 $ s_{m,n}$
只经过二维高斯过滤后点 $(x_{m},y_{n}) $ 像素变为 \[ s_{m,n}^{'}=\frac{1}{(2m+1)(2n+1))}\sum_{p=0}^{2m+1}\sum_{q=0}^{2n+1}{s_{p,q}\cdot{g_{p,q}}} \]
如果原图经过 \(x\) 轴的高斯滤波核大小为 \(2m+1\) ,其中: \[ G_{x}(x)=\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{x^{2}}{2\sigma}} \] 于是点图像变为一个长为 $ 2n +1$ 的向量。不妨记为 $ = [y_0,...,y_{2n+1}]^{T}$
其中 \[ y_{i} = \frac{1}{2m+1}\sum_{k=0}^{2m+1}{G_{x}(i-m)\cdot{s_{k,i}}} \] 再经过\(y\) 轴的高斯滤波核大小为 \(2n+1\) 其中: \[ G_{y}(y)=\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{y^{2}}{2\sigma}} \]
\[ s_{m,n}^{''}=\frac{1}{2n+1}\sum_{q=0}^{2n+1}{y_q\cdot{G_y(q-n)}}\\ =\frac{1}{(2m+1)(2n+1))}\sum_{q=0}^{2n+1}{\sum_{k=0}^{2m+1}{G_x{(i-m)}G_y{(q-n)}}\cdot{s_{k,q}}}\\ =\frac{1}{(2m+1)(2n+1))}\sum_{k=0}^{2m+1}{\sum_{q=0}^{2n+1}{G_x{(i-m)}G_y{(q-n)}}\cdot{s_{k,q}}}\\ =\frac{1}{(2m+1)(2n+1))}\sum_{k=0}^{2m+1}{\sum_{q=0}^{2n+1}}{G(i-m,q-n)\cdot{s_{k,q}}}\\ =\frac{1}{(2m+1)(2n+1))}\sum_{k=0}^{2m+1}{\sum_{q=0}^{2n+1}}{s_{k,q}\cdot{g_{k,q}}}=s_{m,n}^{'} \]
$ Q E D$
均值滤波
均值滤波则可认为高斯核里值恒为1的滤波方式。